Hello everyone. This page is about working with a two by two table in the statistical programming language R.

 

Sections

 

 

Creating Sample Data

 

I start with creating sample (fake) data where males and females are surveyed whether or not they like sushi or not.

 

# Contingency Tables In R
# Book: Extending The Linear Model With R By Julian J Faraway

# Creating a Sample Table: Do You Like Sushi By Gender?
# gl() generates factor levels

library(ggplot2)

counts <- c(19, 24, 18, 21)
gender <- gl(n = 2, k = 1, length = 4, labels = c("Male", "Female"))
interest <- gl(n = 2, k = 2, length = 4, labels = c("Yes", "No"))

survey_data <- data.frame(counts, gender, interest)

survey_data
##   counts gender interest
## 1     19   Male      Yes
## 2     24 Female      Yes
## 3     18   Male       No
## 4     21 Female       No

 

From the survey data, you can easily create bar graphs with the ggplot2 package in R.

 

#### ggplot2 Graphs


# Data Visualization Of Contingency Table With ggplot2 (Stacked Bar Graph):

ggplot(data = survey_data, aes(x = interest, y = counts, fill = gender)) + 
  geom_bar(stat = "identity") + 
  labs(x = "\n Answer", y = "Counts \n", 
       title = "Interest In Sushi By Gender \n",
       fill = "Gender") +
  theme(plot.title = element_text(hjust = 0.5),
        axis.title.x = element_text(face="bold", colour="blue", size = 12),
        axis.title.y = element_text(face="bold", colour="blue", size = 12),
        legend.position = "bottom")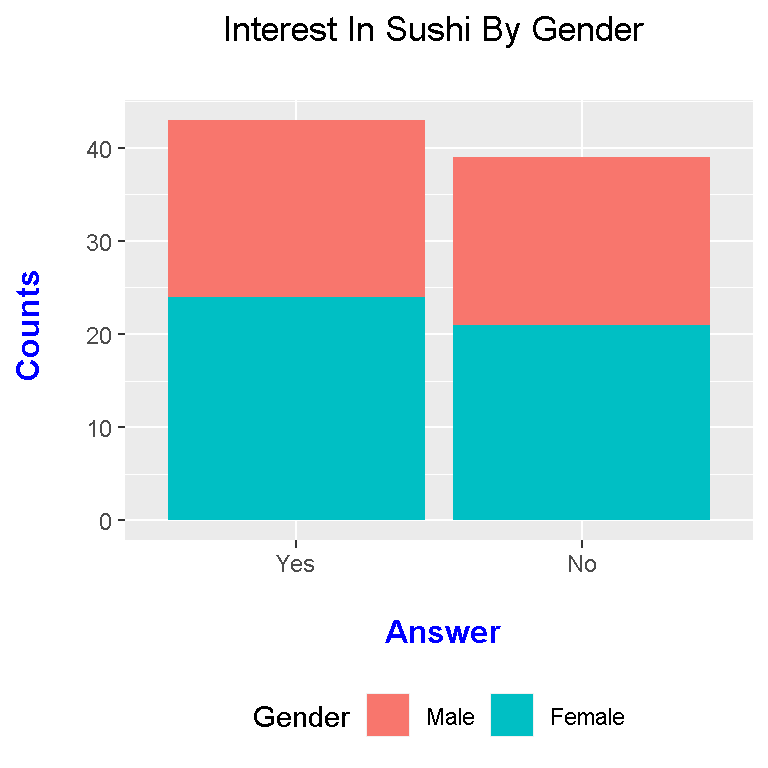

 

The above plot is a stacked bar graph. An alternative to the above would be side by side bar graphs.

 

# Data Visualization Of Contingency Table With ggplot2 (Side By Side Bar Graph):

ggplot(data = survey_data, aes(x = interest, y = counts, fill = gender)) + 
  geom_bar(stat = "identity", position = "dodge", colour = "black") + 
  scale_fill_brewer(palette = "Pastel1") +
  labs(x = "\n Answer", y = "Counts \n", 
       title = "Interest In Sushi By Gender \n",
       fill = "Gender") +
  theme(plot.title = element_text(hjust = 0.5),
        axis.title.x = element_text(face="bold", colour="blue", size = 12),
        axis.title.y = element_text(face="bold", colour="blue", size = 12),
        legend.position = "bottom")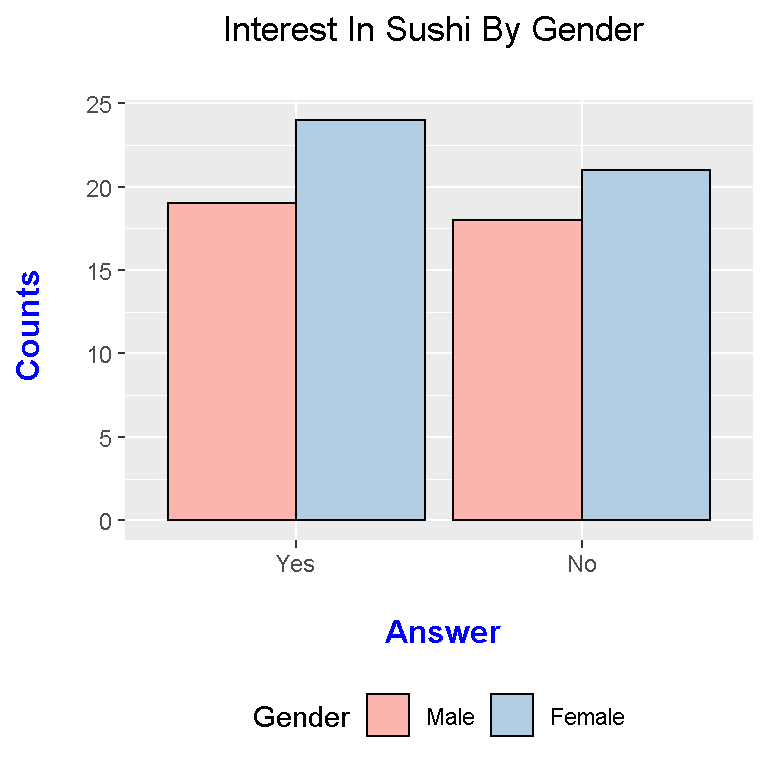

 

I have also changed the colour palette to mix things up.

 

A Two By Two Contingency Table

 

Instead of the long format from the beginning, you can display the table as a two by two contingency table.

 

### Contingency Tables (2 by 2 Case)

conting_table <- xtabs(counts ~ gender + interest)

conting_table
##         interest
## gender   Yes No
##   Male    19 18
##   Female  24 21

 

From this contingency table, you can create a mosaic plot.

 

# Mosaic Plot (Base R):

mosaicplot(conting_table, color = c("red", "green"), main = "Mosaic Plot",
           xlab = "Gender", ylab = "Answer")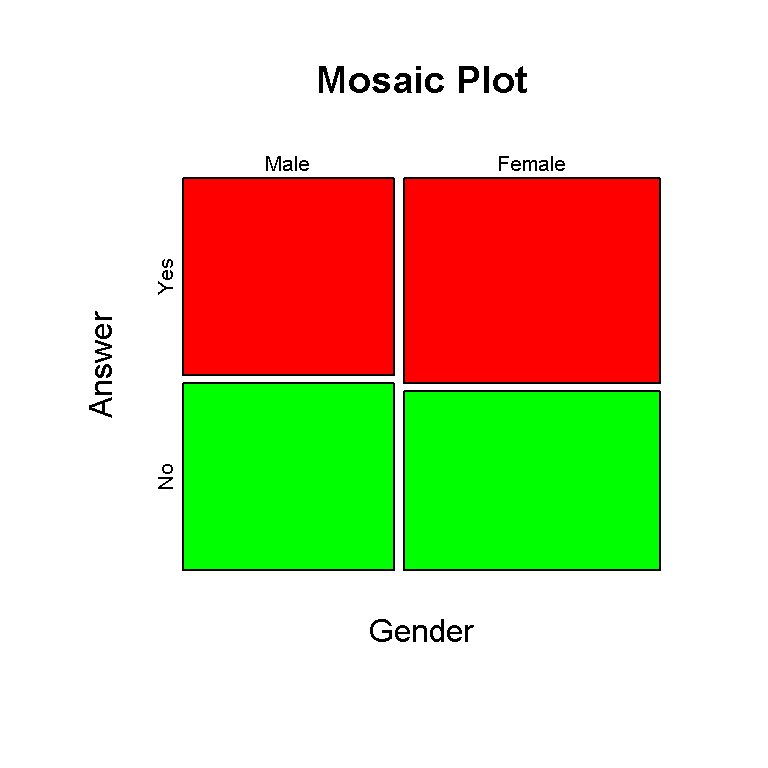

 

Since the counts are really close to each other, it is hard to see a difference between the tile sizes.

An alternate moasic plot comes from the vcd package in R.

 

# Mosaic Plot (vcd package):

library(vcd)

mosaic( ~ gender + interest , data = conting_table,
        highlighting = "gender", highlighting_fill=c("lightblue", "pink"))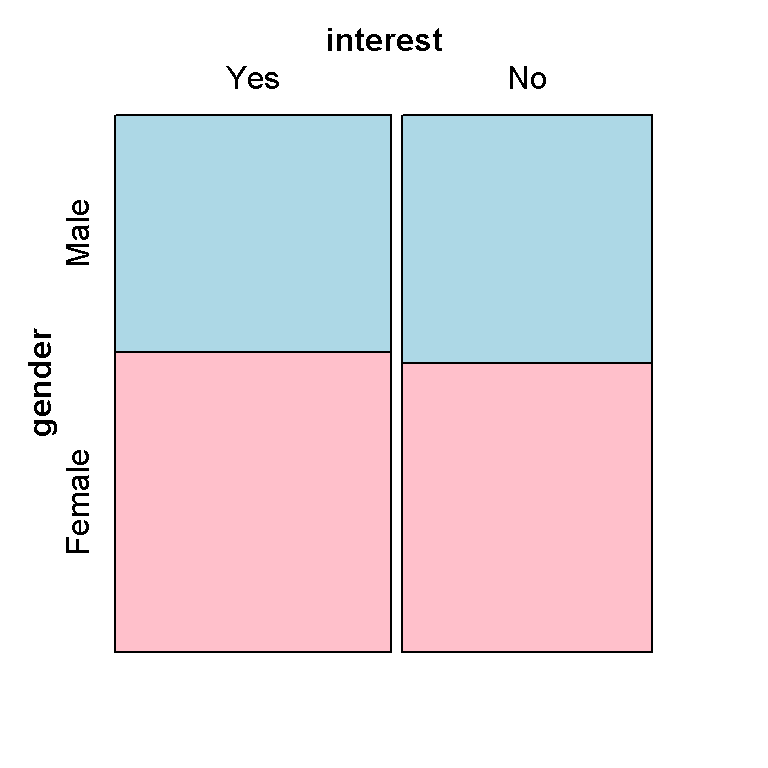

 

Other than the colours and labels, this mosaic plot does not look that much different. Also, I have not figured out how to adjust the label titles and such.

 

Poisson Regression

 

The counts are at least zero (non-negative) and are whole numbers. When dealing with a two by two table, linear regression does not really work. With this data, a Poisson regression model is used.

In R, the glm() function is used where glm stands for generalized linear model. Make sure to indicate family = "poisson" in the glm() function.

 

# Poisson Regression 

poisson_model <- glm(counts ~ gender + interest, family = "poisson", data = survey_data)

summary(poisson_model)
## 
## Call:
## glm(formula = counts ~ gender + interest, family = "poisson", 
##     data = survey_data)
## 
## Deviance Residuals: 
##        1         2         3         4  
## -0.09168   0.08261   0.09557  -0.08726  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   2.96540    0.19516  15.195   <2e-16 ***
## genderFemale  0.19574    0.22192   0.882    0.378    
## interestNo   -0.09764    0.22113  -0.442    0.659    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1.008909  on 3  degrees of freedom
## Residual deviance: 0.031979  on 1  degrees of freedom
## AIC: 25.474
## 
## Number of Fisher Scoring iterations: 3

 

References