The Distance Between Two Points
This topic is about the distance between two points in the two dimensional system.
Suppose we are given a point \(A\) with the co-ordinate (\(x_1\), \(y_1\)) and a point \(B\) with the co-ordinate (\(x_2\), \(y_2\)). We want to find the distance between point \(A\) and point \(B\).
The distance from point \(A\) to point \(B\) is:
\[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
This distance formula is derived from the Pythagorean Theorem with the \(c^2 = a^2 + b^2\) formula. \(c\) is the longest side opposite to the right angle in the right angled triangle.)
Here is a diagram illustrating the geometric intuition behind the formula.
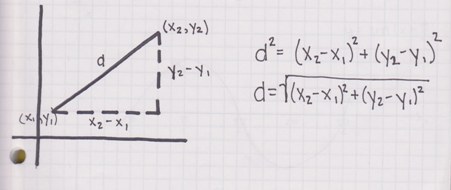
Examples
Example One
Given the point \(A\) as (-1, 2) and \(B\) as (3, 0), the distance between point \(A\) and point \(B\) is:
\[d = \sqrt{(3 - (-1))^2 + (0 - 2)^2} = \sqrt{(4)^2 + (- 2)^2} \]
\[d = \sqrt{16 + 4} = \sqrt{20} = \sqrt{4 \times 5} = 2 \sqrt{5} \]
Example Two
Suppose that the point \(A\) is (-2, 10) and the point \(B\) is (0, 4), the distance between point \(A\) and point \(B\) is:
\[d = \sqrt{(0 - (-2))^2 + (4 - 10)^2} \]
\[d = \sqrt{(2)^2 + (- 6)^2} = \sqrt{4 + 36} = \sqrt{40} = \sqrt{4 \cdot 10} = \sqrt{4} \sqrt{10} = 2 \sqrt{10}\]