Right Angle Triangles & SOH CAH TOA

Table Of Contents

 

• Right Angle Triangles
• Finding Angles & Side Lengths
• SOH CAH TOA Memory Aid
• Examples

 

Right Angle Triangles

A right angle triangle has three sides and three angles with one of the three angles being a 90 degree (right) angle. The three angles inside a (right) triangle add up to 180 degrees. Also, the sides of the right angled triangle obey the formula \(c^2 = a^2 + b^2\) (Pythagorean Theorem) where \(a\), \(b\) and \(c\) are side lengths of the triangle. (Recall that \(c\) is the hypotenuse and the longest side of a right angle triangle.

Here is an example of a right angled triangle:

 

Image Source

Image Source: http://kineticmaths.com/images/7/76/Findangle.jpg

 

Finding Angles and Side Lengths

When dealing with triangles, we sometimes do not know all the angles and all the side lengths of a triangle. If we are given just enough information (i.e. 2 angles and 1 side length), we can use the following formulas to determine the unknown angle(s) and the unknown side length(s).

The sine of an angle \(\theta\) (theta) is the ratio of the side length opposite to the angle \(\theta\) over the length of the hypotenuse. The equation is as follows.

 

\[ \sin(\theta) = \dfrac{Opposite}{Hypotenuse} \]

 

The cosine of an angle \(\theta\) (theta) is the ratio of the side length which is adjacent to the angle \(\theta\) over the length of the hypotenuse. Note that the adjacent side to the angle \(\theta\) is NOT the hypotenuse.

 

\[ \cos(\theta) = \dfrac{Adjacent}{Hypotenuse} \]

 

The tangent of an angle \(\theta\) (theta) is the ratio of the side length which is opposite to the angle \(\theta\) over the side length which is adjacent to the angle \(\theta\).

 

\[ \tan(\theta) = \dfrac{Opposite}{Adjacent} \]

 

SOH CAH TOA Memory Aid

The three formulas can be hard to memorize and follow. A very neat memory aid is SOH CAH TOA. In SOH, the letter S refers to the sine function, the letter O refers to the side length opposite to the angle \(\theta\) and H refers to the hypotenuse side length. The same logic applies to CAH and TOA.

Here is a picture which provides a good summary.

Source: http://www.mathwarehouse.com/trigonometry/images/sohcohtoa/sohcahtoa-all.png

 

Examples

These examples will show how SOH CAH TOA can help in finding unknown side lengths and angles of right angled triangles. The pictures are my own and from my phone.

Example One

In the given picture, we have a right angle triangle with known side lengths and just the known right angle which is angle C.

 

 

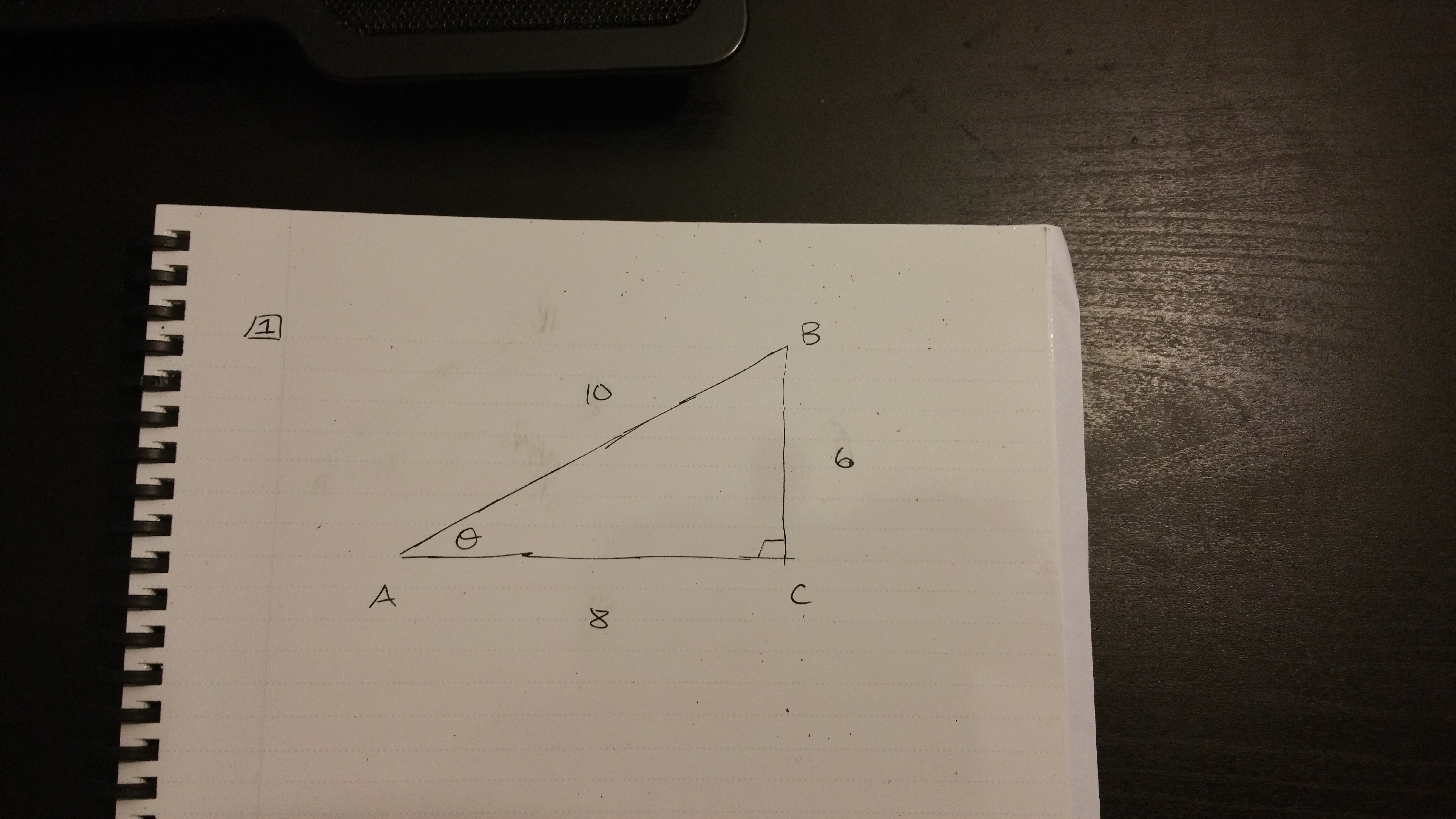
Referring to the angle \(\theta\) we can determine the ratios using sine, cosine and tangent.

 

\[ \sin(\theta) = \dfrac{Opposite}{Hypotenuse} = \dfrac{6}{10} = 0.6\]

\[ \cos(\theta) = \dfrac{Adjacent}{Hypotenuse} = \dfrac{8}{10} = 0.8\]

\[ \tan(\theta) = \dfrac{Opposite}{Adjacent} = \dfrac{6}{8} = 0.75\]

 

We have the ratios but not the angle \(\theta\). To find the angle \(\theta\) we need to use the respective inverse trigonometric function. For example, the inverse sine function \(\sin^{-1}(x)\) would be used to find the angle \(\theta\) given a (valid) numeric value \(x\).

 

\[\sin(\theta) = 0.6\] \[\sin^{-1}(\sin(\theta)) = \sin^{-1}(0.6)\] \[ \theta \approx 36.87^{\circ} \]

 

\[\cos(\theta) = 0.8\] \[\cos^{-1}(\cos(\theta)) = \cos^{-1}(0.8)\] \[\theta \approx 36.87^{\circ} \]

 

\[\tan(\theta) = 0.75\] \[\tan^{-1}(\tan(\theta)) = \tan^{-1}(0.75)\] \[\theta \approx 36.87^{\circ} \]

 

Note that the inverse function of the original function is the argument inside the function. In this case, the inverse trigonometric function of the trigonometric function is the angle \(\theta\). Since the angle \(\theta\) is found, we can now find the angle B. Angle B would be \(180^{\circ} - 36.87^{\circ} - 90^{\circ} = 53.13^{\circ}\).

 

Example Two

In this second example, we have only one known side length and know two of three angles in this right triangle.

 

 

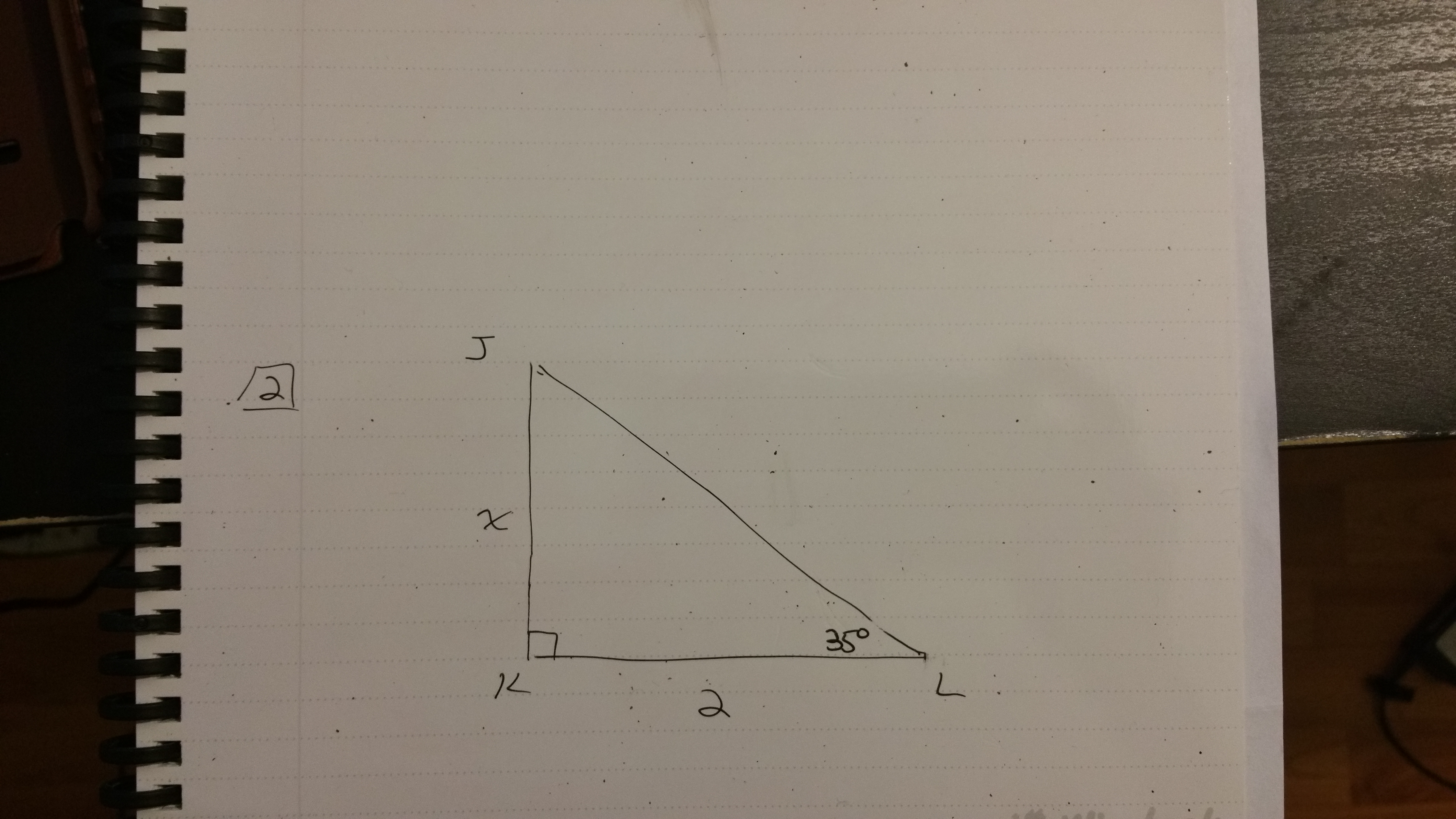
The side \(KL\) is known at 2 units with angle L at \(35^{\circ}\) and angle \(K\) being a right angle. The angle \(J\) can be determined as \(180^{\circ} - 35^{\circ} - 90^{\circ} = 55^{\circ}\).

One way of finding the side length \(x\) is to use the tangent ratio. In this case, \(x\) is adjacent to the angle \(55^{\circ}\) and the side \(KL\) is the opposite side at length 2. Solving for \(x\) gives us:

 

\[\tan(55^{\circ}) = \dfrac{Opposite}{Adjacent} \] \[ \tan(55^{\circ}) = \dfrac{2}{x}\] \[x \tan(55^{\circ}) = 2\] \[x = \dfrac{2}{\tan(55^{\circ})} \] \[x \approx 2 \div 1.428148 \] \[x \approx 1.4004 \]

 

Another way of solving for \(x\) is using the tangent of \(35^{\circ}\). The adjacent side of angle \(35^{\circ}\) is \(KL\) with length 2 and the opposite side length is \(x\).

 

\[ \tan(35^{\circ}) = \dfrac{Opposite}{Adjacent} \] \[\tan(35^{\circ}) = \dfrac{x}{2}\] \[2 \tan(35^{\circ}) = x\] \[2 (0.7002) \approx x \] \[ 1.4004 \approx x \]

 

Assuming the tangent formula is used correctly when solving for the unknown side length \(x\), the choice of (acute) angle does not matter too much.

If we had wanted to find the length of the hypotenuse instead of \(x\), we would use the cosine of \(35^{\circ}\).