This article will be about absolute values. This topic is somewhat tricky for those new to this topic. The images below were produced from the statistical programming language R with the ggplot2 package.

 

The Absolute Value

 

The absolute value of a real number \(x\) is the non-negative part of \(x\). It is expressed as \(|x|\). Sometimes it is referred to the modulus and can be thought of as a distance from zero.

The simplest case of absolute values is with numbers. Here are some examples.

 

\[\displaystyle |3| = 3\]

\[\displaystyle |-3| = 3\]

\[\displaystyle |-120| = 120\]

\[\displaystyle - |120| = - 120\]

\[\displaystyle |0| = 0\]

\[\displaystyle |-1 \cdot 0| = |0| = 0\]

\[\displaystyle |(-2)^2 | = |4| =4\]

 

So far we have dealt with absolute value of numbers and not variables. We now generalize and present the formal definition.

 

\[\displaystyle |x| = \begin{cases}x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}\]  

Here is a visual of the absolute function centered at \(x = 0\).

 

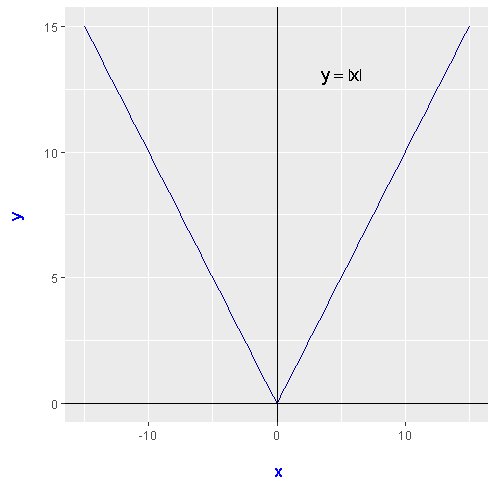
example-one

 

 

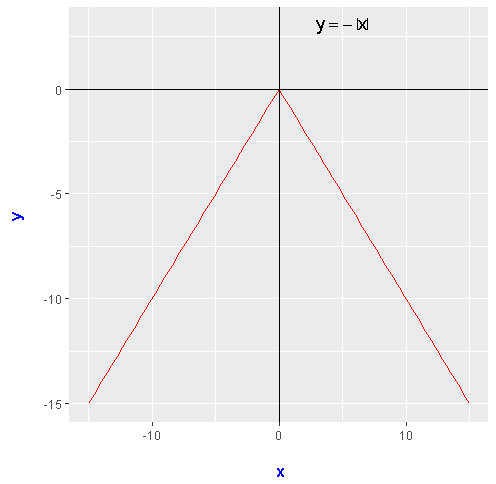
The absolute function is an example of a piecewise function. This type of function depends on the value of \(x\). It is not like linear functions where it is a smooth line for all \(x\) values. If we had \(-|x|\) then the picture above would be upside down and would look like a hat.

 

example-two

 

We now consider intercepts with the \(x\) variable inside the absolute value. If we had \(|x - 7|\) then the origin point at (0,0) from \(|x|\) would be shifted to the right 7 units to the point (7, 0) for \(|x - 7|\). If we had \(|x + 2|\) then the origin point at (0,0) from \(|x|\) would be shifted to the left 2 units to the point (2, 0) for \(|x - 7|\). Refer to the pictures below as a visual aid.

 

example-three

 

example-four

 

Any vertical shifts would have numbers outside the absolute value function. For example, \(|x| + 3\) would shift the every point from \(|x|\) up by 3 units.

 

example-five

 

Domain and Range

 

For the absolute function \(|x|\), the domain is all real numbers for \(x\). The range for \(|x|\) is for all positive numbers and zero.

Properties

 

There are properties associated with the absolute value function. Here are a few.

\[\displaystyle |x| \geq 0\]

\[\displaystyle |x| = 0 \text{ if and only if (iff) } x = 0\]

\[\displaystyle |x \cdot y| = |x| \cdot |y|\]

\[\displaystyle |x + y| \leq |x| + |y| \hspace{0.5in} \text{ (Triangle Inequality)}\]

 

These two properties come in handy when dealing with inequalities. (The constant \(a\) is a real number.)

 

\[\displaystyle |x| \leq a \iff -a \leq x \leq a\]

\[\displaystyle |x| \geq a \iff x \geq a \text{ or } x \leq -a \]

 

For example if we have \(|x - 5| < 2\), we can solve for \(x\) as follows:

\[\displaystyle |x - 5| < 2\]

\[\displaystyle -2 < x - 5 < 2\]

\[\displaystyle -2 + 5 < x < 2 + 5\]

\[\displaystyle 3 < x < 7\]

 

Here is another example where we have \(|x - 1| \geq 3\). The second property is used.

 

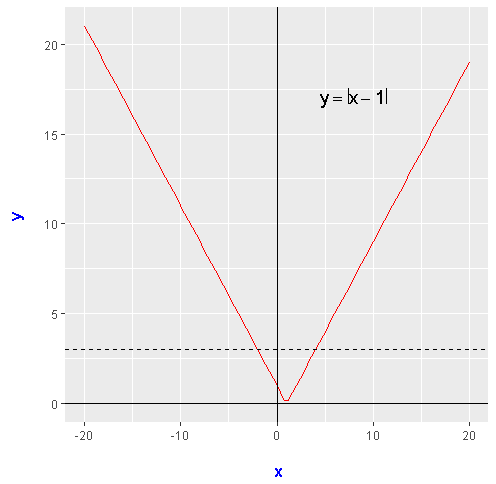
inequal02

 

\[\displaystyle |x - 1| \geq 3\]

\[\displaystyle (x - 1) \geq 3 \text{ or } (x - 1) \leq -3\]

\[\displaystyle x \geq 4 \text{ or } x \leq -2\]

 

Notes

 

There are more things that can be said about the absolute value of \(x\). The topic of absolute values and complex numbers are not mentioned here.